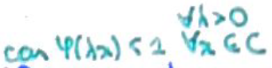Ensemble polaire \(C^\circ\) de \(C\)
Ensemble des Forme linéaires de \(E\) qui sont \(\leqslant1\) sur \(C\).$$C^\circ=\{\varphi\in E^*\mid \forall x\in C,\varphi(x)\leqslant1\}$$

• \(C\) doit être Fermé, convexe et contenir \(0\)
    
• on note \(\mathscr C(E)\) l'ensemble des tels sous-ensembles de \(E\)
• on a alors \(C^\circ\in\) \(\mathscr C(E^*)\)
    
• en particulier, \(C^\circ\) est un Fermé pour la Topologie faible
• dualité polaire : \(C=\{x\in E\mid\forall \varphi\in C^\circ,\varphi(x)\leqslant1\}\)
    
• conséquence : tout ensemble convexe
  Fermé est faiblement
  Fermé
• si \(E\) est réflexif, alors on a \(C=\) \(C^{\circ\circ}\)
• pour les Cônes, le polaire est une ramification du concept d'Orthogonal
    
• pour un Cône
  convexe
  Fermé \(C\), on a : $$\begin{cases} C+C^\circ=H\\ C\cap C^\circ=\{0\}\\ C^{\circ\circ}=C\end{cases}$$

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Quel est l'ensemble polaire d'un Cône \(C\) ?
Verso: $$C^\circ=\{\varphi\in E^*\mid \forall x\in C,\varphi(x)\lt 0\}$$
Bonus:

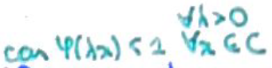
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Quel est l'ensemble polaire d'un evn \(C\) ?
Verso: $$C^\circ=\{\varphi\in E^*\mid\forall x\in C,\varphi(x)=0\}$$
Bonus:

Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Quel est l'ensemble polaire de \(C=B^\prime_E(0,1)\) ?
Verso: $$C^\circ=B^\prime_{E^*}(0,1)$$
Bonus:
Carte inversée ?:
END

Démontrer \(\subset\) :

Cela vient directement, par définition de l'ensemble polaire.

Démontrer \(\supset\) :

On va procéder par contraposée.

Cela vient alors directement en appliquant le Théorème de séparation stricte à \(C\) et à \(\{x_0\}\).

Montrer que si \(C\) est un convexe
Fermé d'un evn, alors il est faiblement
Fermé.

S'il contient \(0\), alors il peut être écrit comme une intersection de demi-espaces via l'écriture avec l'Ensemble polaire.

Sinon, on peut le translater puisque les propriétés se conservent.